AMERICAN RIFLEMAN GUN TESTS
We are interested, here, in the American Rifleman, AR, reported accuracy of sets of five, 5-shot groups.
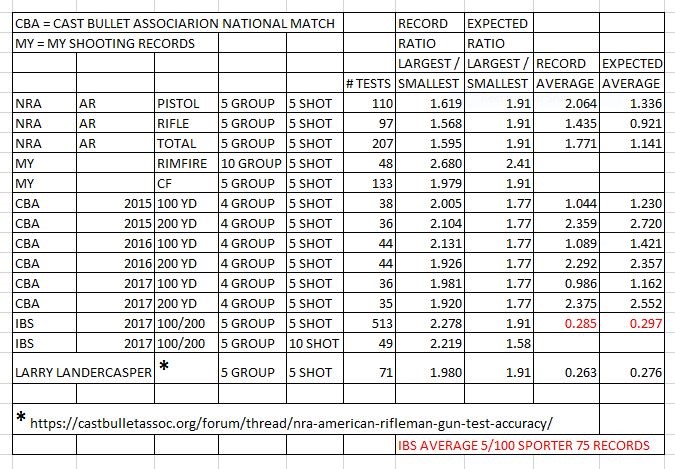
The NRA magazine, “American Rifleman”, publishes the results of gun tests. These tests include accuracy tests, generally for group size of sets of five 5-shot groups. Group Sizer is the distance between centers of the two furthest-apart target holes in a group. The group size measures for each set are: smallest group, largest group and average group size.
If we assume that shot location is distributed NORMAL, then we know the relationships between the three AR measures, can calculate the EXPECTED values of some measures, and compare them with RECORD measures.
With the AR RECORD measures and some calculation, we find that:
The EXPECTED long-term average ratio of largest group / smallest group in sets of five, 5-shot groups is 1.91.
For 207 AR tests ending with the 10/2018 AR, the average RECORD ratio is 1.595.
The EXPECTED long-term average of group size of sets of five, 5-shot groups is 1.141.
For 207 AR tests ending with the 10/2018 AR, the average RECORD average is 1.771.
Because the differences are so large, the sample sizes are large, and calculations of other reported results support the assumption; I conclude that the AR results are probably false.
(The AR data is similar to describing a room as 12 feet long, 20 feet wide, and 180 square feet.)