Tom G
posted this
11 April 2021
Hi John,
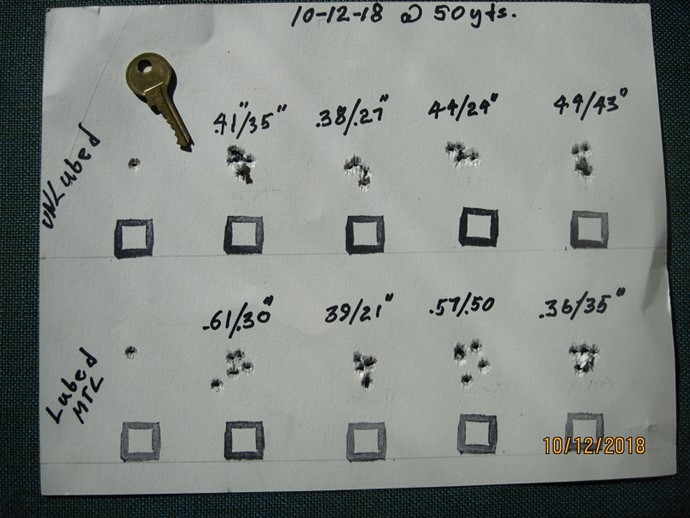
I applaud you for your continued work in trying to evaluate the ways we gage the accuracy of our cast bullet shooting. Your last post piqued my interest in the subject again. For some reason, I recently was thinking of how we evaluate our level of precision and if we are on the right track. For reasons of competition, we measure 5 and 10 shot groups and gage the quality by measuring the two furthest shots from each other. That seems to work to a degree and is probably the best way to conduct a competition within the constraints of time etc. to have a match. But the question arises as you have pointed out; What is the best way to measure the actual performance of our gun/load/shooter? Should we or should we not include fliers or outliers. If so, how much weight should be give to them in establishing the overall accuracy of a load?
In the lost paragraph of your last post, you mention ignoring or throwing out the outlier shots in some of the groups we shoot in gaging the quality or "true accuracy" of a load. You bring up a good point on what to do with the outliers or fliers in a group. My opinion is that we need to always include them in the calculations. Using the two widest shots method of evaluating groups or average accuracy is not, in my estimation a good way to include the outlier shots.
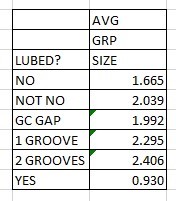
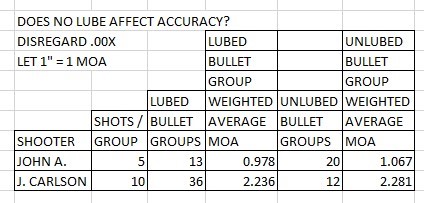
First, I believe that shooting 5 and 10 shot groups and then averaging them together is not the best way to evaluate the overall accuracy of a gun/load combination. i suggest that a better way is to shoot all the sample shots into the same group and increase the sample size. Increasing the sample size increases the percent of confidence of the conclusions made from analyzing the group.
Many years ago, I'm almost 79 now, I was working for Ford Motor Company as a Quality Control Analyst. Part of my job was to evaluate the quality levels of production operations for compliance with the established dimensional tolerances of the component parts and completed assemblies. I routinely had a person go out into the factory and take a sample of a part or assembly and gage all of them and record the data. I would then take the data and run it in a computer program that broke down the distribution of the recorded dimensions and basically put them into a bell shaped curve and predicted with a certain level of confidence what the larger population of parts would fall under as far as how many percent fell within the tolerances allowed on the design drawings.
We were dealing with a stack up of tolerances when we started assembling a bunch of parts into, let's say, an engine distributor, We knew that over 99% of the parts would likely fall into an acceptable range and work well when mated to other engine parts. We also anticipated getting the occasional "outlier" that due to a stack up of too many max dimension parts would end up too big or the opposite, too small. The sample size was in the range of 250 samples and that yielded a percent of confidence that was in the very high 99 % range. In other words, the result of analyzing the data could be expressed as " I am 99.6 % confident that 98,2% of the parts will fall within the design limits". Or something like that. I'm pretty sure that now, 50 years later, they probably do it a little different.
With that in mind, I feel that what we are trying to accomplish is much the same in measuring the accuracy of a load on paper. In the above example, we measured every part. We didn't throw out any part that was outside the core group of dimensions. In measuring the quality of a group, we need to include all the fliers or outliers in the group as part of the group. As you mentioned, we could throw out some percentage of outliers as unexplained fliers and grade the group without them. But that would be ignoring science in my humble opinion and distorting the actual data that we collected. Let's face it, they were part of the group and we need to find a way to include them in the calculations for the quality of the group.
If we look at extreme spread of a group, we find that including the outliers in it really distorts the level of quality of the group excessively and that's not acceptable.
I'm thinking that a better way of evaluating the group size is to shoot all the shots into one group. Use a sample size of say 25 shots instead of 5 five shot groups. Include all shots in the analysis and not throw out any fliers. Find a way to establish a reference point in the group and then measure the distance each shot is from the reference point. Add up all the distances and divide by the number shots shot. The result would be an average distance from the reference point. Use that as the quality level of the group.
If we could find a way to establish the average center of the group, that would probably be the best way to establish the reference point from which all shots are compared. That way, an outlier shot would have no more effect on the final calculated quality level of the group than any other shot would have.
I've seen similar methods like this for evaluating groups in the past. Keep in mind that this method is just giving us a level of dispersion from a central location, not how well the shots fell in relation to an intended point of aim. In other words we could say we are looking at the consistency of the rifle/load to put a certain number of shots together in one spot. I think this method or one similar to it would allow us to include outliers in the calculations as they should be without giving them more weight than they deserve. It seems to me that a method such as this would tell us with more certainty how well a certain load is doing in relation to other loads.
Just my $ 0.02 worth.
Tom